Arrays, Explained in 4 Minutes

Arrays are one of the most commonly used data structures, and probably one of the first data structures most software engineers learn about.
*An array is a type of data structure that stores a collection of elements. Each element in the array has a specific index that can be used to access it. Arrays are often used to store data in a specific order.*
Explanation using a real-world problem
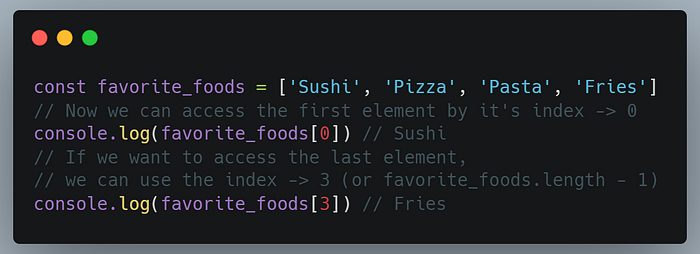
For example, let’s say you have a list of your favorite foods. You could store this list in an array. The first element in the array would be your first favorite food, the second element would be your second favorite food, and so on. You could then access each food in the array by its index.
Accessing Time
If we let the size of the array be n, we can access an element in the array by its index in O(1) time.
This is possible because elements are stored at contiguous locations in memory. This direct access can be seen in the code example above.
*For the remainder of this article we will assume the size of the array is n*
Search Time
If we would like to find an element in the array, we can do this in O(n) time.
This is because, in the worst case, we have to iterate through the entire array to find the element. This can be seen in the code example below.

The search time can be improved if we assume that the array is sorted.
This is possible because we can use binary search to find the element in O(log n) time given a sorted array.
For more information on binary search, see my post about the binary search algorithm
Insertion Time
The time needed for inserting an element into an array depends on the index we want to insert the element at.
If we would like to insert the element at the end of the array, and we know the length of the array is n, then we can insert the element in O(1) time.
This is because the elements already stored in the array can remain in the same location in memory, and the new element can be inserted at the end of the array (at index n+1).
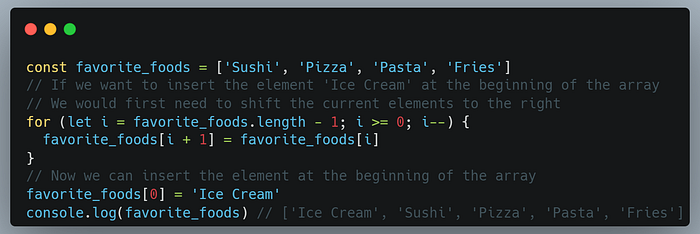
If instead, we would like to insert the element at the beginning of the array, the insertion would require O(n) time.
This is because the elements already stored in the array have to be shifted to the right to make room for the new element. As can be seen in the code example below.
Deletion Time
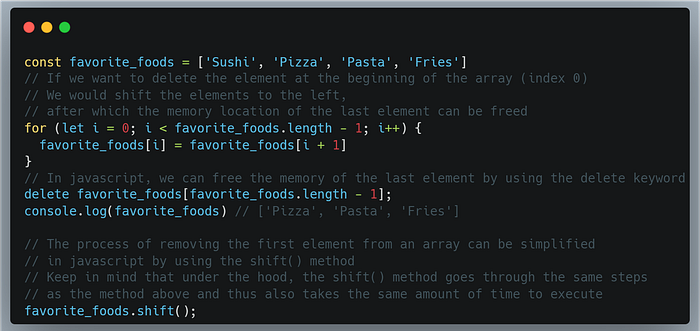
The time needed for deleting an element from an array, as with insertion, depends on the index we want to delete the element from.
Following the same logic as insertion, the worst-case time for deletion is O(n), which occurs when we delete the first element in the array.
This is because the elements after the deleted element have to be shifted to the left to fill the gap.
The Series
This article is part of a new series, wherein I explain complex algorithms and data structures in a clear and concise manner — whilst consuming the least amount of reading time.
Make sure to either follow me, subscribe to my newsletter, or take a look at the article mentioned above to get updates on the series.
More content at PlainEnglish.io. Sign up for our free weekly newsletter. Follow us on Twitter and LinkedIn. Join our community Discord.

